Función inyectiva, sobreyectiva y biyectiva
Función inyectiva:
La función “Inyectiva” o “Uno a uno”, es la situación en la
que si a los elementos del conjunto X(Dominio), le corresponden los elementos
del conjunto Y(Codominio) de f(función). Es decir, cada elemento del
conjunto Y tiene una sola preimagen proveniente de X, o así mismo, en el conjunto
X los elementos no pueden tener la misma imagen cada uno.
Si es inyectiva
Como cada línea horizontal
intercepta en un solo punto Si es inyectiva.
Función sobreyectiva:
Una función es catalogada como sobreyectiva cuando está aplicada a todo el codominio, es decir, cuando cada elemento del conjunto Y pertenece como mínimo una imagen del conjunto X. Si la imagen es el conjunto de los reales, la función es sobreyectiva.
Ejemplo:
f(x)=x*2+3
Dom: ℝ (Todos los reales)
Rec: ℝ (Todos los reales)
Esta función es sobreyectiva, ya que la imagen de la función pertenece al conjunto de los reales.
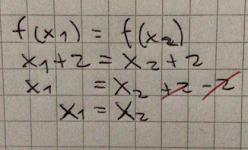





Comentarios
Publicar un comentario